果冻的猿宇宙

在前面, 我们探讨了泛型范式在解决重复性问题上的应用, 在这里, 将继续探讨泛函范式在解决重复性问题上的作用.

注: 关于"泛函(functional)"这一名称, 前面说了, 泛型的本质是"参数化类型", 那么, 按照这一思路, 泛函的意思也可以理解为"函数的参数化"或者现在时髦的所谓"函数式编程(functional programming)"吧!

当然, 你可以有自己的看法, 这里用这种比较概括性的说法可以使得标题等比较简短, 我也承认, 很多时候, 想取一个简短又准确的名字是不容易的.

从高斯的求和故事说起

据说高斯(Gauss, 德国数学家)同学小时候, 有一次老师让大家求从 1 加到 100 的和, 当其它小朋友还在埋头苦算时, 我们的小高斯同学却很快给出了结果: 5050!

老师和其它小伙伴都惊呆了:

原来聪明的高斯同学注意到了一个事实, 那就是: 1+100=101,2+99=101, ... 50+51=101, 总共有 50 组, 所以 50 * 101 = 5050, Done!

现在我们用程序来解决这一问题, 我们就不用那些奇淫技巧了, 简单粗暴一个 for 循环求和, 以计算机速度之飞快, 妥妥秒杀我们的高斯同学:

/** 求普通和 */
public static int sum() {
	int sum = 0;
	for (int i = 1; i <= 100; i++) {
		sum += i;
	}
	return sum;
}

更多的求和

现在, 让我们来看更多的求和问题, 除了普通的求和, 我们还可能想求比如平方和, 那么可以这样写:

/** 求平方和 */	
public static int sum() {
	int sum = 0;
	for (int i = 1; i <= 100; i++) {
		sum += i * i;
	}
	return sum;
}

如果想求立方和, 可以这样写:

/** 求立方和 */
public static int sum() {
	int sum = 0;
	for (int i = 1; i <= 100; i++) {
		sum += i * i * i;
	}
	return sum;
}

自然, 我们的计算机在做起这些反复的类似的工作来是毫无怨言而且是又快又好的, 可是一再类似的重复工作却会让我们人类心生厌倦.

一再重复的模式

让我们具体看看, 重复的 bad smell 坏味道很容易就能嗅到, 请看下面的对比:

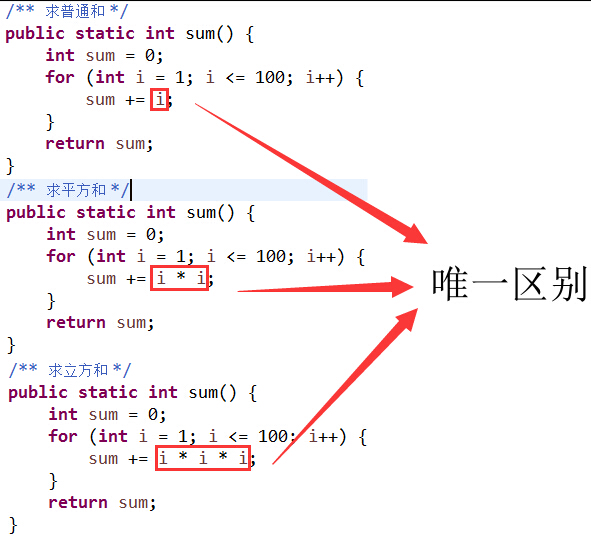
不难注意到, 除了 += 右边存在差异外, 代码的其它地方都是一样的!

从字面看, 也不难发现重复:

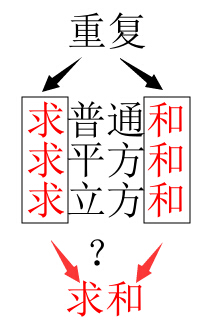
从求普通和, 到求平方和, 再到求立方和, 自然, 我们是不能忍受这种一再重复的. 我们的语言能否表达出"求和"本身这一抽象概念, 而不是限于求具体的某种和? 如何去消除这种模式的重复呢?

去重的初步设想

按照我们之前在泛函范式中的谈论, 很容易就能想到: 能否把这些差异参数化, 外部化呢? 比如这样:

public static void main(String[] args) {
	sum(i);
	sum(i * i);
	sum(i * i * i);
}

public static int sum(Object exp) {
	int sum = 0;
	for (int i = 1; i <= 100; i++) {
		sum += exp;
	}
	return sum;
}

当然, 以上代码在 Java 下是不能编译通过的, 但它的确清晰的表达出了我们的意图. 再仔细想想, 我们想要的效果大概是这样:

public static int sum(Function f) {
	int sum = 0;
	for (int i = 1; i <= 100; i++) {
		sum += f(i);
	}
	return sum;
}

public static int identity(int i) {
	return i;
}

public static int square(int i) {
	return i * i;
}

public static int cube(int i) {
	return i * i * i;
}

我们想要的是传递一个函数(或者说方法)进来, 然后在我们的求和函数中调用它.

public static void main(String[] args) {
	sum(identity);
	sum(square);
	sum(cube);
}

很遗憾, 以上代码在 Java 中依然是不能编译通过的.

如果是使用 javascript 这样的语言, 这样写已经差不多了. 不过这里不打算列举具体的代码实现.

不过, 再做些调整, 就能达到我们的意图了.

传统的解决方案

自然, 我们也可以一下子跳到函数式的解决方案上去, 这在 Java 1.8 支持了 lambda 方式之后也并不是什么问题了；或者你直接使用一个原生就支持函数式的语言那也 OK, 比如 javascript.

不过, 这里还是打算一步一步的来, 这样有助于我们理清事情的来龙去脉, 更加清晰的体会到函数式的好处.

如果你没有耐心, 可以直接直接跳过此章节. 我也承认, 有时这种技术文章不好写, 写得详细, 基础好的同学可能觉得啰嗦；写得简略, 读者可能又觉得跳跃性太大, 不好理解. 这里做个折中, 写得是尽量详细, 但也分成了不同的章节, 你可以根据需要取舍.

if-else, naive 的方式

最简单也最容易想到的方式就是用 if-else 来判断不同情况, 这种方式的代码如下:

public static void main(String[] args) {
	int idSum = sum("identity");
	int sqSum = sum("square");
	int cbSum = sum("cube");
	
	System.out.print(idSum + " " + sqSum + " " + cbSum);
}

public static int sum(String type) {
	int sum = 0;
	for (int i = 1; i <= 100; i++) {
		int temp = 0;
		if ("identity".equals(type)) {
			temp = i;
		} else if ("square".equals(type)) {
			temp = i * i;
		} else if ("cube".equals(type)){
			temp = i * i * i;
		} else {
			// TODO error
		}
		sum += temp;
	}
	return sum;
}

很简单, 就是通过一个 String 的类别参数, 然后用 if-else 的方式来判断, 它在一定程度上解决了重复, 比如循环的代码只出现了一遍, 但其弊端也是很明显的.

首先, 尽管参数传递进来后就不会再变了, 可是循环中还是每次都会去判断, 影响了性能, 某种程度上看也是一种重复.

如果我们把判断放在 for 循环外面, 那又不得不重复 for 循环那些代码, 跟之前差不多.

其次是一旦有新的求和方式要添加, 又不得不修改这些代码.

它违反了所谓的开闭原则(OCP: Open Closed Principle), 软件中的对象(类, 模块, 函数等等)应该对于扩展是开放的, 但是对于修改是封闭的. (open for extension, but closed for modification)

通常会建议使用多态来代替这些条件判断, 参见 Martin Fowler 的这篇文章: https://refactoring.com/catalog/replaceConditionalWithPolymorphism.html

多态策略(Polymorphism)

if-else 的方式很容易想到, 但弊端也很明显, 我们需要更好的解决方案.

实际上前面的初步设想已经很接近满足需求了, 只不过传统的 Java 语言坚持"一切都是对象", 对象在 Java 中是**第一级(first-class)**的, 可以做参数, 可以放在变量中, 可以作为返回值等等.

关于第一级(first-class)的概念, 后面还会具体介绍.

但它不能支持或者说不直接支持传递函数或方法的引用. 为此, 我们不得不引入一个叫 MyFunction 的接口, 里面有一个简单的 apply 方法, 接受 int 参数, 返回一个 int 结果:

public interface MyFunction {
	public int apply(int i);
}

public static int sum(MyFunction f) {
	int sum = 0;
	for (int i = 1; i <= 100; i++) {
		sum += f.apply(i);
	}
	return sum;
}

然后, 弄几个类实现这一接口:

class Identity implements MyFunction {
	@Override
	public int apply(int i) {
		return i;
	}
}

class Square implements MyFunction {
	@Override
	public int apply(int i) {
		return i * i;
	}
}

class Cube implements MyFunction {
	@Override
	public int apply(int i) {
		return i * i * i;
	}
}

这样, 想进行不同的求和时, new 出具体的类即可:

public static void main(String[] args) {
	int idSum = sum(new Identity());
	int sqSum = sum(new Square());
	int cbSum = sum(new Cube());
	
	System.out.println(idSum + " " + sqSum + " " + cbSum);
}

同时, 它也具有良好的可扩展性, 想进行新的求和, 可以创建出新的类并实现接口即可.

泛型是参数化多态, 接口和继承则是子类型多态, 不过这里不打算去探讨它们的细节.

这种方式大概是 GoF 说的"策略模式"(strategy).

GoF: gang of four, 就是写<<设计模式>>一书的四个家伙(四人帮)

不过, 由于不少模式有些相似, 我也记不清了这到底是策略模式还是模板方法, 还是其他, 亦或都不是, 如果你比较清楚, 欢迎留言.

不过, 它的缺陷在这种简单需求中也体现得很明显, 有许多的类要定义, 大量重复的**脚手架(scaffold)**的代码.

应该说, 借助于现代的 IDE, 书写这些代码也不是很难了, 不过有些人可能还是会觉得不爽.

毕竟, 反复地写那些样板代码某种程度也是一种重复性的问题.

匿名内部类(Anonymous Inner Class)

如果对于简单的需求不想定义太多的类, 可以使用匿名类的方式:

public static void main(String[] args) {
	// 匿名类方式
	int idSum = sum(new MyFunction() {
		@Override
		public int apply(int i) {
			return i;
		}
	});
	
	int sqSum = sum(new MyFunction() {
		@Override
		public int apply(int i) {
			return i * i;
		}
	});
	
	int cbSum = sum(new MyFunction() {
		@Override
		public int apply(int i) {
			return i * i * i;
		}
	});
	
	System.out.println(idSum + " " + sqSum + " " + cbSum);
}

这种方式一定程度上减轻了某些重复繁琐的工作, 但依旧还是有不少的样板代码, 不够简洁, 重点也不突出.

反射方式(Reflection)

假如我们的代码中已经存在诸如求平方, 求立方等工具类的代码,

public class MathUtil {
	public static int identity(int i) {
		return i;
	}

	public static int square(int i) {
		return i * i;
	}

	public static int cube(int i) {
		return i * i * i;
	}
}

而且我们也不想再定义什么接口及子类型, 尽管这在一定程度也解决了我们的问题, 但回到我们最初的意图, 我们就想传入一个方法, 然后调用一下它而已.

这大概类似于 C++ 等语言中的函数指针.

Java 并不直接支持传递函数引用, 但通过反射的方式, 也还是能够间接得做到这一点的. 我们来看下:

public static void main(String[] args) throws Exception {
	// int.class 表示方法参数的类型
	int idSum = sum(MathUtil.class.getMethod("identity", int.class));
	int sqSum = sum(MathUtil.class.getMethod("square", int.class));
	int cbSum = sum(MathUtil.class.getMethod("cube", int.class));
	
	System.out.print(idSum + " " + sqSum + " " + cbSum);
}

public static int sum(Method m) throws Exception {
	int sum = 0;
	for (int i = 1; i <= 100; i++) {
		// 第一个参数为 null 表示为静态方法, 没有对象与之关联
		// 返回值为 Object 类型, 所以需要强制类型转换
		sum += (int)m.invoke(null, i);
	}
	return sum;
}

可以看到, 通过反射, 方法也能被参数化了, 这样直接就解决了我们的问题.

当然, 弊端也不少, 比如很多异常要处理:

为求简洁, 示例代码中直接抛出了所有异常, 但真实应用中, 这样做是很草率的.

其次, 直接使用字符串参数, 也没有编译期的检查, 写错了不到运行时也发现不了.

再次, 大量反射的运用也有潜在的性能开销.

总体而言, 至少在这个问题上, 反射方案还是不够简洁优雅, 虽然已经很接近我们最终的意图了. 从根源上讲, 问题出在 Java 不能直接支持所谓的"函数第一级(first-class function)"上.

JCP 社区的大佬们似乎也听到了群众的呼声, 推出的 JDK 8.0 总算是在这个问题上有了交待.

在进一步讲解之前, 我们先简单了解下"函数第一级"的概念.

函数第一级(First-class Function)

一般而言, 程序设计语言总会对计算元素的可能使用方式强加上某些限制. 带有最少限制的元素被称为具有 第一级(first-class) 的状态. 第一级元素的某些"权利或者特权"包括:

• 可以用变量命名；
• 可以提供给过程作为参数；
• 可以由过程作为结果返回；
• 可以包含在数据结构中.

注: 以上说法直接来自<< SICP >>一书中, 这里所谓的"过程", 可以认为就是"方法"或者"函数".

程序设计语言元素的第一级状态的概念应归功于英国计算机科学家 Christopher Strachey.

简单地讲, 函数第一级就是函数可以做参数, 可以作为返回值等等.

高阶函数(Higher Order Function)

有了函数第一级, 一些函数就可以接受函数作为参数, 也可以把函数作为返回值返回, 这样的函数, 我们称之为"高阶函数(higher order function)", 高阶函数可以为我们提供强大的抽象能力, 从而消除一些我们用普通方式不能或者很难消除的重复.

简单讲, 可以认为它们是函数的函数, 用我们前面的话讲, 它们是代码的代码, 抽象之抽象, 模板的模板, 等等.

泛函的解决方案(lambda 式)

有了 JDK 1.8, 有了函数第一级, 我们就可以把 sum 函数定义为一个高阶函数, 它接受一个函数作为参数, 这里用 java.uitl 包下的 Function 类型表示这样一个泛函参数:

public static int sum(Function<Integer, Integer> f) {
	int sum = 0;
	for (int i = 1; i <= 100; i++) {
		sum += f.apply(i);
	}
	return sum;
}

它有个 apply 方法, 但并不需要我们去实现, 传递给它的方法就是它的实现, 所以直接传递一个方法引用给它即可:

public static void main(String[] args) {
	int idSum = sum(MathUtil::identity);
	int sqSum = sum(MathUtil::square);
	int cbSum = sum(MathUtil::cube);
}

注意这里的写法, 类后面跟着两个冒号(::), 然后是方法名.

这里并没有在调用这个方法, 没有括号, 也没有参数, 实际上它就是我们一开始所设想的那种意图, 仅仅是传递一个方法引用而已.

跟反射的方式比较的话, 它不是一个 String, 而更像是一个符号类型(Symbol ), 支持编译器检查, 也支持 IDE 的代码提示, 如果你写错了, IDE 会提示你出错了, 不用像反射那样到运行期才能知道.

这里甚至可以使用所谓的 lambda 表达式, 进行所谓"函数式编程":

int idSum = sum(i -> i);// 求普通和
int sqSum = sum(i -> i * i);// 求平方和
int cbSum = sum(i -> i * i * i);// 求立方和

int dbSum = sum(i -> 2 * i);// 求两倍和
int qrSum = sum(i -> i * i * i * i);// 求四次方和

这里的箭头表达式就是所谓的 lambda 表达式了, 可以看到, 我们可以很轻松地写出求普通和, 平方和, 立方和, 乃至四次方和等等, 几乎消除了所有的脚手架式的代码, 非常简洁优雅.

也可以直接复用 Math 类中的方法:

double sinSum = sumf(Math::sin);

因为 sin 需要 double 的参数, 这里需要调整 sum 的参数为 double:

public static double sumf(Function<Double, Double> f) {
	double sum = 0;
	for (int i = 1; i <= 100; i++) {
		sum += f.apply((double) i);
	}
	return sum;
}

然后还可以直接复用 Math 里的 pow 方法来做平方和立方等等:

double sqSum2 = sumf(i -> Math.pow(i, 2));
double cbSum2 = sumf(i -> Math.pow(i, 3));

总结

可以看出, 引入了函数式编程后, 代码显得直接, 简洁, 优雅. 利用高阶函数的抽象, 我们去除了重复, 消除了耦合.

由于篇幅的关系, 关于泛型与泛函的一个综合总结, 留待下篇再分析.