在前面我们谈论了重复性管理上的一些具体做法, 重点探讨了 泛型范式 在解决重复性问题上的应用. 因为前面的篇幅有很多被具体的代码例子占据了, 所以留到现在这篇做一个归纳总结.
与数学的渊源
应该说, 编程与数学还是颇有渊源的, 或者说它们之间有很多相通的地方. 数学的一个突出特点, 那就是数学家总是在不断寻求更加一般化的表述, 更为抽象的表达. 我们来看一个具体的例子.
数学上有所谓的勾股数, 最知名的就是我们所熟知的"勾三股四玄五"了. 具体而言就是 3^2 + 4^2 = 5^2.
注: 3^2 表示 3 的 2 次方(平方), 因为上标较为麻烦, 其余类似.
类似的正整数组合还有比如: 5^2 + 12^2 = 13^2.
显然, 我们都知道这些都是勾股定理的一些正整数特例而已, 数学家们肯定不会只满足与此, 很早他们就发现了所有的直角三角形都满足一个一般化的表达如下:
a^2 + b^2 = c^2.
这就是所谓的"勾股定理"了.
在西方, 叫"毕达哥拉斯定理"(Pythagorean theorem)
那么, 是否到这里, 事情就结束了呢? 如果你还记得曾经学过的数学, 那么你应该还记得有个东西叫"余弦定理(law of cosines)", 具体如下:
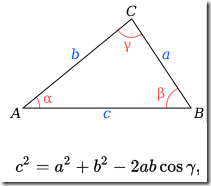
当角度 γ 为 90 度时, 因为 cos(90) = 0, 这样"余弦定理"就简化成了所谓的"勾股定理". 所以, 余弦定理是比勾股定理更加一般化的表述.
3,4,5 和 5,12,13 这些勾股数是勾股定理的特例, 而勾股定理本身又是余弦定理的一个特例.
从勾三股四玄五到勾股定理再到余弦定理, 从特殊到一般, 从一般到更一般, 显然, 数学家从未停止他们抽象的脚步, 总是在追寻更加一般化的定理, 更加普适的定律.
事实上, 这个平面上的余弦定理还可以进一步推广到立体的"四面体(tetrahedron)"上的余弦定理:
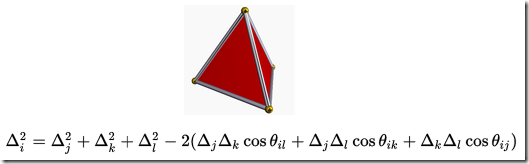
这个就比较深奥, 比较抽象了, 恐怕知道的人也不多, 但数学家们是不会停止的!这个可谓是更加一般化的表述了.
反之, 平面上的余弦定理可以视作为它的一个特例.
类似的例子还有很多, 事实上你在中学里所学的好多定理都还可以进一步推广, 不过因为在形式上也越来越抽象, 很多已经超出了我们普通人的理解能力, 这里也不再去挖掘那些例子了.
所谓的"泛"
现在, 我们来看所谓的"泛", 前面的篇章中也一再说了, 就是一个从特殊到一般的过程:
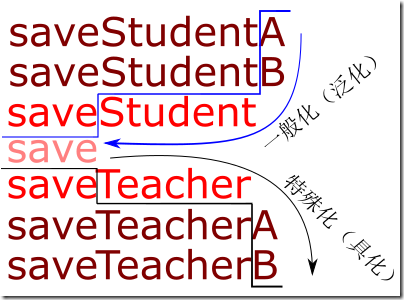
是一个从具体到抽象的过程:
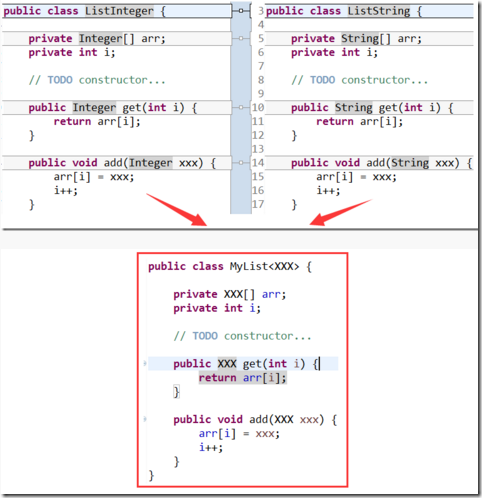
函数已经是一种抽象, 我们还不满足, 我们还要追求更高阶的抽象:
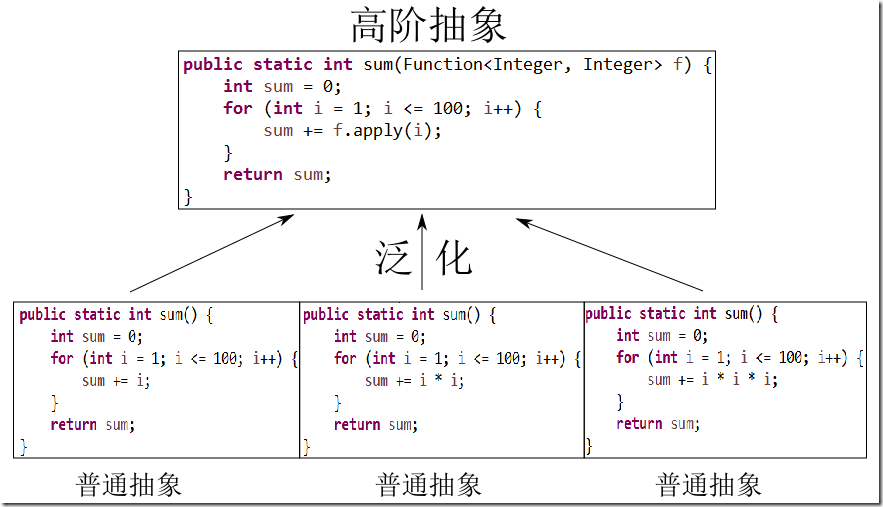
还是那句话, 从特殊到一般, 从一般到更一般!无论是值的硬编码, 类型的硬编码, 还是行为的硬编码, 能够被泛化的, 我们都将其一一参数化, 一般化.
在这一过程中, 我们消除了重复, 得到了极为抽象的代码, 这些对值没有依赖, 对类型也没有依赖, 对具体行为也没有耦合的代码具有极强的普适性. 依靠这些手段, 我们不但消除了眼下的重复, 甚至也消除了未来的重复.
当你写的代码越来越多, 当你思考得越来越深, 你一定对这一点体会越来越深. 或许我们还不能将它清晰的表述出来, 但我相信我们一定会逐渐地感受到, 用陶潜的一句诗来结尾, 可谓是: 此中有真意, 欲辨已忘言!

注: 图片来自互联网. 附上原诗:
饮酒(其五)-- 陶渊明
结庐在人境, 而无车马喧. 问君何能尔? 心远地自偏. 采菊东篱下, 悠然见南山. 山气日夕佳, 飞鸟相与还. **此中有真意, 欲辨已忘言. **
