果冻的猿宇宙

以下是我们的问题:

把 100 元用 50 元, 20 元, 10 元, 5 元, 1 元去换, 总共有几种换法?

形式化(formalize)

为了简化叙述, 把问题记为 coc(100, [50, 20, 10, 5, 1]).

coc: case of change 或者 count of change(change 在英文中有零钱的意思)

为使问题更具有一般性, 参数化具体值, 得到:

caseOfChange(amount, cashList)

其中 amount 为金额, cashList 为零钱列表.

递归分析

前面说到递归分两种情形, 一是基本情形(base case), 二是递归情形(recursive case).

基本情形(base case)

显然, 问题难在零钱种类太多, 如果只有一种零钱, 问题就简单了:

比如 coc(100, [50])==1, 即有一种换法, 也就是换成 2 张 50 的.

又如 coc(50, [20])==0, 即没法换, 2 张 20 够, 3 张又太多.

显然, 结果不是 0 就是 1, 就看能否整除. 根据以上分析, 得出:

caseOfChange(amount, cashList) { 
	// base case
    if (cashList.containsOnlyOneCash()) { // 只有一种零钱时 
        if (amount.canBeChangedWith(cashList.getTheOnlyOneCash())) { // 能换时, 即能整除 
            return 1;
        } else { 
            return 0; 
        } 
    } else {
    	// recursive case, TODO
    }
}

注: 暂时请只专注于描述我们的问题, 现在还不急着考虑具体的实现.

递归情形(recursive case)

因为递归的模式并不是那么明显, 我们还是先回到传统的思路上考虑.

拆分问题

问题难在零钱种类太多, 我们首先考虑能否拆解它.

把大问题分成几个小问题, 或者说把一个复杂问题分成几个简单问题, 这是我们常用的伎俩.

那么怎么分解呢? 我们经常能想到的就是一分为二.

如果我们能找到一种方法, 比方说, 能把 5 种零钱拆成 "1+4", 那么 "1" 可以在 base case 中解决了, 更进一步, 4 又可拆成 1+3, 循环往复, 问题就可解决了.

具体事例

为方便思考, 我们还是用更具象的例子来分析. 比如, 怎么把 coc(100, [50, 20, 10, 5, 1]) 中的 50 拆分出来?

在纸上写下一些具体的换法, 经观察可以有两种换法:

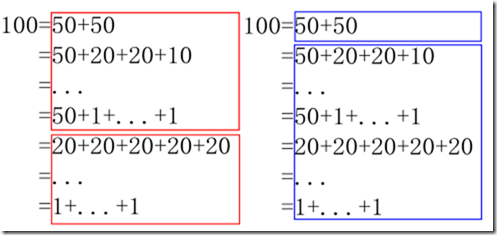
换零钱两种分类方法

一种如红色部分, 分成"用了 50 的"和"没用 50 的".

一种如蓝色部分, 分成"完全只用 50 的"和"不完全用 50 的"(这等于说还是没把 50 拆分出来).

所以, 红色那种更好一点, 它的另外一部分已经彻底与 50 无关了.

不过, 与我们想像的把 5 拆成 1+4 不同, 这里是把 5 拆成 5+4.

它意味着把 [50, 20, 10, 5, 1] 分成了 [50, 20, 10, 5, 1] 和 [20, 10, 5, 1]. 因为前者除了 50 之外依然还用了其它.

考虑一下集合中的"并"操作. [50, 20, 10, 5, 1] U [20, 10, 5, 1] = [50, 20, 10, 5, 1], 对吧, 希望你还能记得. 所以反之你确实可以把它视作某种分解.

现在可以把结果写成两部分之和, 形式化的表达如下:

coc(100, [50, 20, 10, 5, 1])=cocWith50(100, [50, 20, 10, 5, 1]) + cocWithout50(100, [50, 20, 10, 5, 1])

其中: cocWith50 表示 "用了 50 的", cocWithout50 则为 "没用 50 的".

找到一个递归!

显然, 现在已经不是递归了, coc 已经变成了 cocWith50 和 cocWithout50, 星星已经不是那个星星了.

不过你要是再仔细看看上面图中红色部分的下半身:

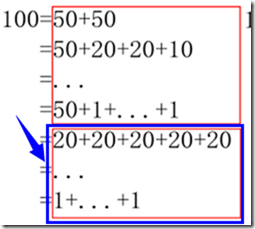
换零钱子部分递归

也即是前面等式中右边第二部分的 cocWithout50(100, [50, 20, 10, 5, 1])), 它不就是 coc(100, [20, 10, 5, 1]) 吗?

观察 cocWithout50(100, [50, 20, 10, 5, 1]), 既然方法声称不使用 50, 参数 [50, 20, 10, 5, 1] 里还带了 50 不就没用了吗?

所以 cocWithout50(100, [50, 20, 10, 5, 1])=cocWithout50(100, [20, 10, 5, 1]),

然后, 既然参数里已经不带 50, 方法不就没必要强调 without50 了吗?

所以 cocWithout50(100, [20, 10, 5, 1])=coc(100, [20, 10, 5, 1])!

至此可以得到以下等式:

coc(100, [50, 20, 10, 5, 1])=cocWith50(100, [50, 20, 10, 5, 1]) + coc(100, [20, 10, 5, 1])

子问题中的一个已经向着原问题递归了, 而且第二个参数 cashList 在减小, 这意味着递归有收敛的可能!

临门一脚

现在激动地畅想一下, 如果我们能把等式右边第一部分的 cocWith50 也能向 coc 靠拢, 那不就大功告成了吗?

怎么往 coc 这条大腿上靠呢? 我们不妨从结果出发, 所谓向它靠拢, 也即是要寻求一种等价关系, 使得:

cocWith50(100, [50, 20, 10, 5, 1])==coc(?, [?..?])

观察一下, 等式左边有三个元素:

cocWith50,
100,
[50, 20, 10, 5, 1]

从结果出发, cocWith50 要变成 coc, 这个是我们的目标.

但这样就会丢掉一个特性, 那就是"with50"(它强调了每种换法一定要用到50), coc 方法显然是没这种强调的；

所以其它两个元素的变化必须体现这个特性或者说至少做出某种呼应.

那么, 我们还有两个元素可以变. 而且从要让递归收敛的角度考虑, 它们应该是一种递减的变化.

现在看第二个元素, 100 能怎么变? 或者说 100 能变吗? 毕竟你是要拿 100 去换呀!不太明朗, 我们先看看第三个.

第三个元素, cashList, 能怎么变呢? 既然要递减, 我们无非希望能去掉 list 中的一些, 让我们看看:

cocWith50 点名了要 50, 不能少,

但也没说其它的如 20, 10, 5, 1 之类的就不要呀, 所以也不能少!(从图中也能直观看出, 这些零钱都可能会用到)

另外, 也不清楚如何去呼应 "with50" 这一丢失的特性. 看来我们只好把目光再次投向第二个元素"100"了:

毕竟, 你能依靠的也就这哥俩了, 100 会是我们的救命稻草吗?

让我们大胆猜测一下, 让 100 变成 "100-50", 也即是认定:

cocWith50(100, [50, 20, 10, 5, 1])=coc(100-50, [50, 20, 10, 5, 1]) =coc(50, [50, 20, 10, 5, 1])

注: 最后的 50 是由 100-50 得到的, 恰好也是 50, 但与零钱列表中的 50 是不同的.

我们当然不是胡乱猜测, 有两个理由:

cocWith50 变到 coc, 去掉了 "with50", 我们也在 100 里减去 50, 正好呼应了这一变化.
这使得参数在减小, 符合递归要求参数递减的要求.

当然, 我们想要的其实是 cashList 的递减, amount 的减小不能让我们递归到 base case 上.

但从另一角度看, 如果 amount 能不断减小, 将导致 cashList 中的一些零钱比 amount 还大, 这将间接导致 cashList 的递减, 也即递归将会收敛.

比如 100 递减到了 20, 那么 coc(20, [50, 20, 10, 5, 1])=coc(20, [20, 10, 5, 1]), 因为 50 比 20 还大, 所以去掉也没影响了.

自然, 我们还需要寻求更加明显的理由来支持我们的猜测. 紧扣 "with50" 这一特性, 从图片观察:

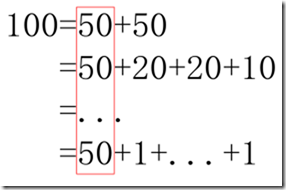
换零钱带有50的换法

显然, 既然每种不同换法都带了 50(红色部分), 那么去掉它之后, 不同的换法彼此间还是保持不同(蓝色部分). 所以:

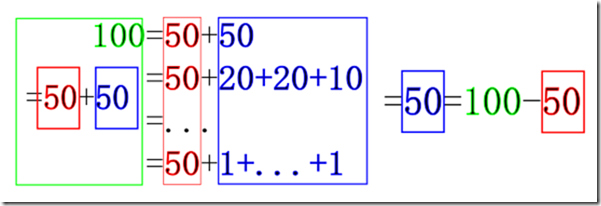
换零钱带有50的换法拆分

那么, 100-50 的意义在哪, 现在就很明确了, 因为每种换法都带了 50, 所以减去它不影响等价性. 所以:

cocWith50(100, [50, 20, 10, 5, 1])=coc(100-50, [50, 20, 10, 5, 1])=coc(50, [50, 20, 10, 5, 1]) , 猜测被证实!

由于 100-50 恰好为 50, 两个 50 容易误解, 我们举另外一个例子, 比如把 50 用 [20, 10, 5, 1] 去换, 则如下图所示:

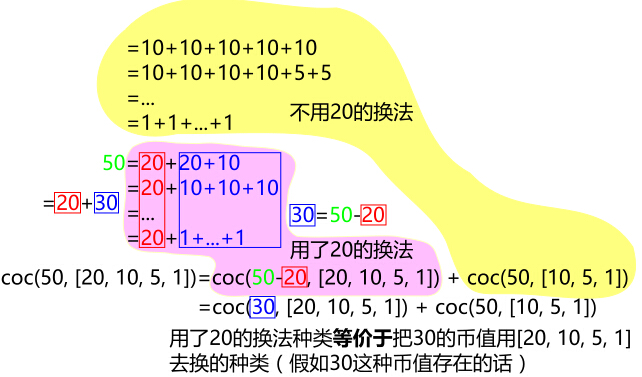
recursive_coc50

综合之有:

coc(100, [50, 20, 10, 5, 1]) = coc(100-50, [50, 20, 10, 5, 1]) + coc(100, [20, 10, 5, 1])

递归模式已经被归纳出来. 参数化, 抽象化后:

coc(A, [C1, C2…Cn]) = coc(A-C1, [C1, C2…Cn]) + coc(A, [C2, C3…Cn]);

即:

caseOfChange(amount, cashList) { 
	// base case
    if (cashList.containsOnlyOneCash()) { // 只有一种零钱时 
        if (amount.canBeChangedWith(cashList.getTheOnlyOneCash())) { // 能换时, 即能整除 
            return 1;
        } else { 
            return 0; 
        } 
    } else {
    	// recursive case
    	return caseOfChange(amount.subtractBy(cashList.getFirstCash()), cashList)
        	+ caseOfChange(amount, cashList.newCashListWithoutFirstCash());
    }
}

其中:

amount.subtractBy(cashList.getFirstCash()), 正如方法名字所暗示那样, 表示"金额减去第一个零钱"；
cashList.newCashListWithoutFirstCash() 表示"去掉第一个零钱后的新零钱列表".

至此, 主体的结构已经基本 OK 了, 不过, 还遗留一个问题, 递归情形中的第一部分还无法收敛, 还需要增加一些额外判断, 即当金额比零钱列表中的第一个还小时, 就减小零钱列表的元素, 这样就能向着 base case 归约了.

或者换种思路, 让金额一直递减, 直到它为 0 甚至为负时我们再作出决定. 我们来看看这意味着什么.

手动演算

根据递归模式, 我们也可以手动地演算一下. 以简单的 "把 10 元换成 5 元与 1 元" 为例, 有 coc(10, [5, 1])=3.

具体为 5+5, 5+1+1+1+1+1, 1+1+1+1+1+1+1+1+1+1 三种.

公式推演如下:

coc(10, [5, 1])

=coc(10-5, [5, 1]) + coc(10, [1])

=coc(5, [5, 1]) + 1

=coc(5-5, [5, 1]) + coc(5, [1]) + 1

＝coc(0, [5, 1]) + 1 + 1

那么现在问题来了, coc(0, [5, 1])=?

显然, 根据最终结果为 3, 所以 coc(0, [5, 1])=1, 也即用 0 元去换, 有一种换法.

这可能会让人觉得有些不好理解, 现实中没人去拿 0 元去换.

如果观察上述的推算过程, 还出现了 coc(5, [5, 1]), 即 5 元又拿 5 元与 1 元去换, 显然, 现实中也不会发生这样的换法.

其实前面也出现了 coc(50, [50, 20, 10, 5, 1], 50 元又用了 50 元去换.

但我们知道, 之所以出现这种情况, 是等价替换造成的, coc(5, [5, 1]) 是经过一次约减后的中间结果, 而 coc(0, [5, 1]) 则是经过两次约减后得来的, 它实际就是原来的 "5+5" 这种换法.

金额为 0 的情况

可以用另一种角度来看待这个问题, 以 coc(10, [5, 1])=3 为例, 这里实质是什么呢?

10 = 2 × 5 + 0 × 1, 相当于 5 + 5, 也即 10 元能换成 2 张 5 元加 0 张 1 元, 只不过我们通常省略后者.

10 = 1 × 5 + 5 × 1, 相当于 5+1+1+1+1+1, 也即 10 元能换成 1 张 5 元加 5 张 1 元.

10 = 0 × 5 + 10 × 1, 相当于 1+1+1+1+1+1+1+1+1+1, 也即 10 元能换成 0 张 5 元加 10 张 1 元, 只不过我们通常省略前者.

所以 =3 实质就是有三种系数的组合: (2, 0), (1, 5), (0, 10).

我们不考虑系数为负的情况, 否则就有无数种可能了. 如:

10 = 3 × 5 + (-5) × 1

10 = 4 × 5 + (-10) × 1

=…

那么 0 = 0 × 5 + 0 × 1, 相当于有一种且唯一一种系数组合 (0, 0), 也即 0 元能换成 0 张 5 元加 0 张 1 元.

不考虑系数为负的情况, 那么就不可能有其它组合了, 因为两个零钱都是正数.

实际上, coc(0, [50, 20, 10, 5, 1])也是 1 种.

系数组合为 (0, 0, 0, 0, 0). 不管有多少零钱种类, 只要用 0 元去换, 都有一种且唯一一种换法.

显然, 只要能整除, 反复约减之下就能得到 0.

同理: coc(5, [5, 1]) 有两种系数组合 (1, 0), (0, 5).

金额为负数的情况

反之, 如果不能整除, 反复约减之下就会得到负数, 如 coc(50, [20, …]), 那么, 三次约减之后就会出现形如 "coc(-10, [20, …]", 那么, 这种情况就认为有 0 种换法, 即不可换.

最终结果

综上, 增加两种 base case 的判断, 程序就能收敛了, 最终形式化的结果如下:

caseOfChange(amount, cashList) { 
    // base case
    if (amount.isNegative()) { // 负数 
        return 0; 
    } 
    if (amount.isZero()) { // 0元 
        return 1; 
    }
    if (cashList.containsOnlyOneCash()) { // 只有一种零钱时 
        if (amount.canBeChangedWith(cashList.getTheOnlyOneCash())) { // 能换时, 即能整除 
            return 1;
        } else { 
            return 0; 
        } 
    }
    
    // recursive case
    return caseOfChange(amount.subtractBy(cashList.getFirstCash()), cashList)
        + caseOfChange(amount, cashList.newCashListWithoutFirstCash());
}

由于篇幅太长, 将在后面的篇章中给出具体的程序实现并做一些回顾与总结.

递归解决换零钱问题(1)--问题分析

目录