二叉树的遍历是一个数据结构中经常会遇到的知识点, 具体又分为前序, 中序和后序三种.
什么是树?
先来理解一下什么是树, 从一个我们相对熟悉的家谱树(Family Tree)说起吧.
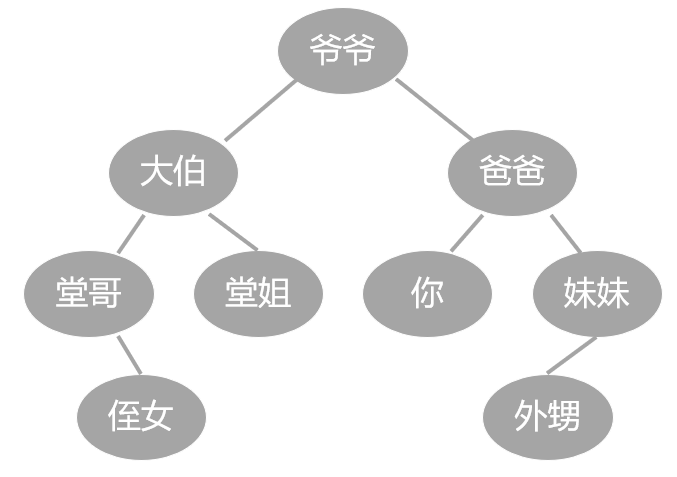
家族的根是爷爷, 然后生了两个娃, 大伯和你爸爸. 继续往下, 有堂哥堂姐, 还有你以及你妹, 等等.
一个家族繁衍下来, 很像一棵树开枝散叶, 当然跟真的树相比, 画出来时通常是倒过来的, 根在上面.
摘要: 利用家谱树的例子深入讲解了二叉树深度优先遍历中的前序遍历, 中序遍历和后序遍历
二叉树的遍历是一个数据结构中经常会遇到的知识点, 具体又分为前序, 中序和后序三种.
先来理解一下什么是树, 从一个我们相对熟悉的家谱树(Family Tree)说起吧.

家族的根是爷爷, 然后生了两个娃, 大伯和你爸爸. 继续往下, 有堂哥堂姐, 还有你以及你妹, 等等.
一个家族繁衍下来, 很像一棵树开枝散叶, 当然跟真的树相比, 画出来时通常是倒过来的, 根在上面.
介绍了在 javascript 中利用 arguments.callee 来实现匿名递归的方式.
递归是一种常见的编程技巧, 实名递归相信大家都不陌生, 但如果想要实现匿名递归呢? 比如想要返回一个匿名递归函数, 又或者是定义一个匿名递归函数并直接调用它, 该怎样去做呢? 本文将来探讨一下它的实现.
我们还是先从实名递归说起吧, 还是用那个最简单的求阶乘的例子:
function fact(n) {
if (n < 2) {
return n;
} else {
return n * fact(n - 1);
}
}
console.log(fact(5));
递归要求自己调用自己, 如果函数有名字, 这就太简单不过了.
摘要: 关于递归表达能力的一个总结.
前面为了保持叙述的流畅, 没有做太多的引申, 把总结推迟到了后面.
补上一些总结, 以防止出现 "下面呢? 下面没有了" 的尴尬.
虽然题目在一开始就暗示了这一点, 但首先, 我们还是要问, 它能用递归解决吗?
有点怀疑精神是好的, 既要低头走路, 更要抬头看路, 以防止发生方向性错误, 导致缘木求鱼的后果.
说这个问题能用递归解决, 这种信心或者判断的依据来自于哪呢?
有人可能知道了, 换零钱这个问题在<<计算机程序的构造和解释>>(SICP: Structure and Interpretation of Computer Programs)一书有这个例子, 而在书上是用递归来解决的.
摘要: 递归解决换零钱问题的具体代码实现, 提供了两种实现, 一种面向对象式, 一种面向过程式, 使用 Java 语言.
在上一篇中, 经过深入分析, 已经得出一个能够递归的形式化的结果, 现在则准备给出一个具体实现.
前述结果如下:
caseOfChange(amount, cashList) {
// base case
if (amount.isNegative()) { // 负数
return 0;
}
if (amount.isZero()) { // 0元
return 1;
}
if (cashList.containsOnlyOneCash()) { // 只有一种零钱时
if (amount.canBeChangedWith(cashList.getTheOnlyOneCash())) { // 能换时, 即能整除
return 1;
} else {
return 0;
}
}
// recursive case
return caseOfChange(amount.subtractBy(cashList.getFirstCash()), cashList)
+ caseOfChange(amount, cashList.newCashListWithoutFirstCash());
}
其实已经大体 OK 了, 基本就差确定一下类型就差不多了.
摘要: 用递归方式解决求换零钱种数的问题.
以下是我们的问题:
把 100 元用 50 元, 20 元, 10 元, 5 元, 1 元去换, 总共有几种换法?
为了简化叙述, 把问题记为 coc(100, [50, 20, 10, 5, 1]).
coc: case of change 或者 count of change(change 在英文中有零钱的意思)
为使问题更具有一般性, 参数化具体值, 得到:
caseOfChange(amount, cashList)
其中 amount 为金额, cashList 为零钱列表.