前面为了保持叙述的流畅, 没有做太多的引申, 把总结推迟到了后面.
补上一些总结, 以防止出现 "下面呢? 下面没有了" 的尴尬.
方向性问题
虽然题目在一开始就暗示了这一点, 但首先, 我们还是要问, 它能用递归解决吗?
有点怀疑精神是好的, 既要低头走路, 更要抬头看路, 以防止发生方向性错误, 导致缘木求鱼的后果.
说这个问题能用递归解决, 这种信心或者判断的依据来自于哪呢?
有人可能知道了, 换零钱这个问题在<<计算机程序的构造和解释>>(SICP: Structure and Interpretation of Computer Programs)一书有这个例子, 而在书上是用递归来解决的.
相似性
在前面的有趣的递归(Recursion), 一些直观的示例中, 展示了一些递归的直观的示例, 还提到了相似性这一点, 递归的东西总是带着点相似性;反之, 如果我们能发现相似性, 那么它也很可能是递归.
以换零钱为例, 100 可以换成 50+20+20+10, 单独拿出 50 也可换成 20+20+10, 你能隐约感觉到一些相似, 尽管还不能明确的说出来.
直观以及与此相关的直觉常常能给我们指明方向, 尽管这种感觉带有很大的主观性及不确定性, 但当我们还无法确定问题的方向时, 它也许能给我们带来一丝线索.
循环
在前面的经典递归分析说到, 循环(迭代)总是可以用递归来解决, 因为递归其实也就是在方法层面的循环. 那么这个问题能用循环解决吗?
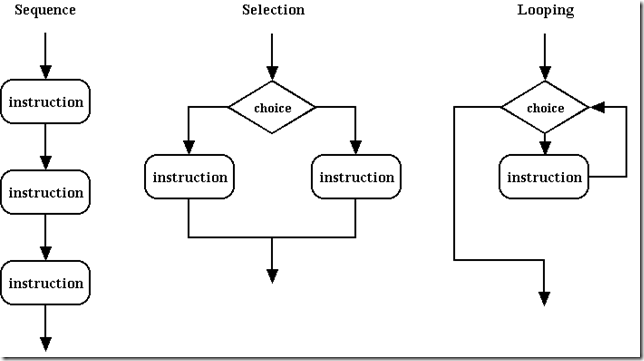
作为计算机科学中的一个伟大远见(洞察力)(great insight)之一的 Boehm and Jacopini’s Insight是这样说的:
Only three rules of grammar are needed to combine any set of basic instructions (verbs) into more complex ones:
只须三种语法规则去组合那些基本的命令就可表述那些更加复杂的过程.
它们是:
- 顺序 (sequence)
- 分支 (selection or choice)
- 循环 (repetition or looping)
考察换零钱问题, 如果不能用循环解决的话, 那么用程序去解决这个问题可能就没什么优势了.
试想如果仅用顺序及分支, 而所谓分支不过就是枚举各种情况, 这样即便能写出程序, 恐怕也是极其臃肿, 而且可能只是特定于某个问题, 不具有普适性.
所以, 如果断定换零钱问题存在循环解法, 那么它也就一定能用递归解决了. L. Peter Deutsch 有句名言:
To iterate is human, to recurse divine.(迭代者人, 递归者神)
所有的程序都可以用三种结构表示出来, 递归本身是一种循环手段, 在递归体的内部又可以包含顺序与分支的情况, 从这个意义上说, 事情其实已经是很明朗的了, 递归方式并不存在什么局限性. 人们很多时候并没有采用它一者可能是习惯问题, 二者则是效率问题.
广义角度
尽管我们可能没有意识到, 很多的问题都可以用递归去表达的. 比如, 秦始皇统一六国使用的远交近攻手段也可写成递归方式:
远交近攻(未统一地区) {
如果(未统一地区.还有离我较远的国家()) {
交往之(未统一地区.离我较远的国家());
消灭之(未统一地区.离我较近的国家());
// 递归, 把原来"离我较远的国家"当成新的"未统一地区"
远交近攻(未统一地区.离我较远的国家());
} 否则 {
消灭之(未统一地区.离我较近的国家());
// 达成统一大业
}
}
以下图片展示了这一过程: (当然了, 与真实的历史过程是有很大区别的, 仅作演示)
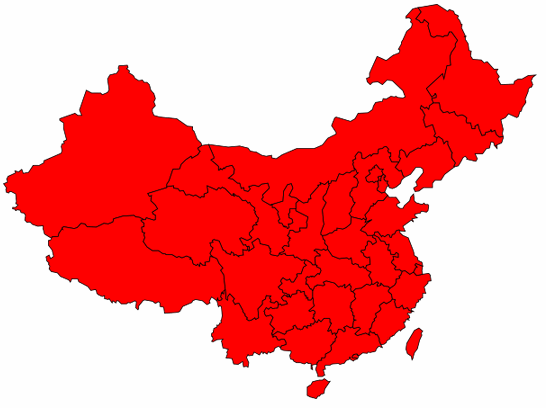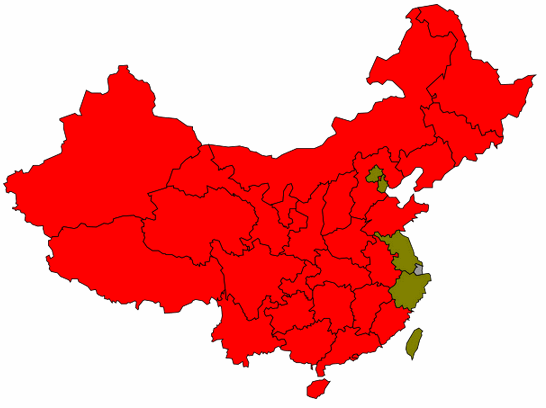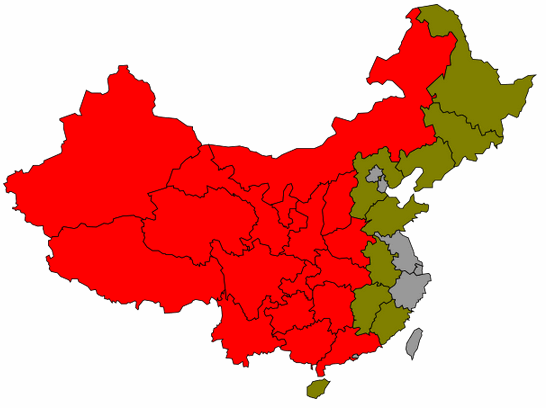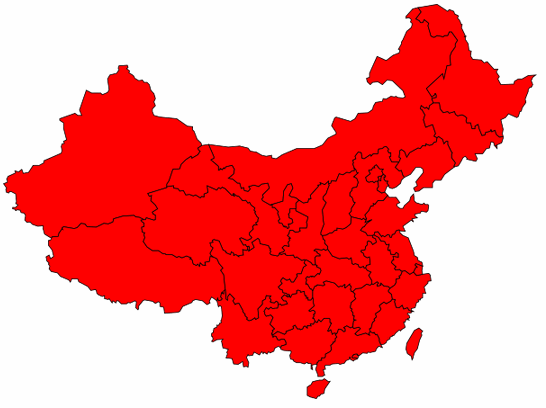
是不是觉得有点扯谈呢? 还是那句话, 只要是循环的重复的过程, 总是可以用递归来表达的.