在前面我们说到了所谓的"计算机科学", 重点在于如何控制大型系统的复杂性.
复杂性本身当然也是个很大的话题, 而一种常见的复杂性的来源则是重复性, 即是由不断的重复所带来的复杂性.
重复性带来的复杂性常被人忽视, 大概是因为一开始它是不起眼的, 而当人们意识到它的存在时可能已经陷入了泥潭.
从心理学说起
下面的一幅图(来自知乎日报), 你一眼就能看出有几个点的是哪些呢?
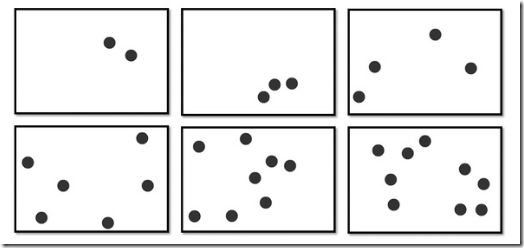
显然, 上面一行你能很容易看出来, 下面一行则有难度了.
心理学上还有一个所谓的"短时记忆的容量"问题:
1956 年, 美国心理学家米勒教授发表了一篇重要的论文, 明确提出短时记忆的容量为 7±2, 即一般为 7, 并在 5 ~ 9 之间波动. 这就是神奇的 7±2 效应.
这在我们日常生活中也不难观察到, 最简单的例子就是有人在电话里报了一个手机号码给你, 多数人都不得不借助纸和笔才能记下来.

一个手机号码, 不过是从 9 再多重复了两次, 到了 11 位, 多数人就无法一下子记住它们了.
所以, 即便是简单的重复, 它的影响也可能是深远的.
一个隐喻场景
让我们来看一个更具体的例子, 先从一个简单的隐喻场景说起, 假如你掉了一根针在你的座位底下, 你要怎么找回它呢?
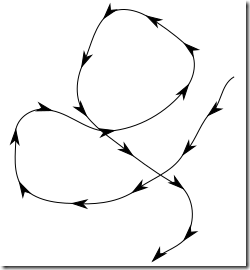
很简单, 你东找找, 西找找, 东找不着, 你就西找, 西也找不着, 你就重复东找, 然后重复西找, 直到你找到为止.
在这种情况下, 你不需要任何的方法论. 以下可能是你寻找的路径:
现在假设针不是掉在了座位底下, 而是在整个房间里, 但你不知道具体哪里, 现在你要怎么找呢?
整个房间与座位底下有什么本质不同吗? 好像没有, 不过是一小块面积重复了更多遍而已, 然而它已经对你的寻找策略造成了冲击.
你还能像之前那样东找找西找找吗? 当然, 你想撞下运气也是可以的, 但你也可能面临重复了几次依旧一无所获的尴尬境地. 此刻, 最保险的方式是遵循如下蛇形的逐行扫描式的排查,
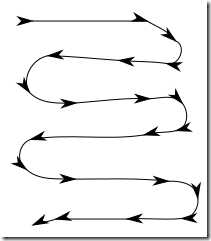
这样你能确保你的寻找时间有一个上限.
现在, 场景再换一下, 假设针不是掉在了房间里, 而是在一个大操场上, 你要怎么找呢?
可以说, 现在那种随机游走式的东找找西找找再也不适合了, 首先一次随机找到的概率太低了, 然后反复随机的话, 你不能确切知道那些地方你已经找过了.
一个大操场与一间房间本质上还是一样的, 只是面积重复了更多次, 但我们以往的寻找策略则彻底不行了, 即便是那种蛇形的逐行扫描式的排查也有很大风险了.
对于这种情况, 首先最好是操场划出块来:
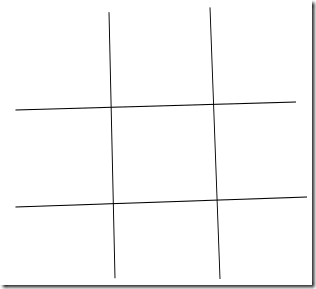
然后是一些簿记工作:
然后一块一块寻找, 在每一小块中, 重复房间的寻找策略:
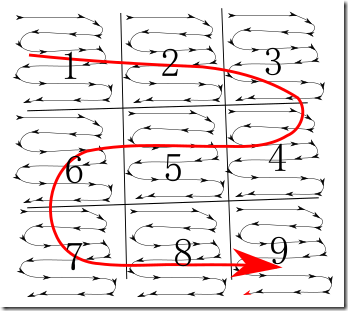
找完了则在簿记上标记一下, 直到找到为止. 如果一遍过完了还没有找到, 则清除所有标记, 重复再查找.
还有可能发动更多的人, 把不同块分配给不同的人, 进行并发式的寻找.
不难看出, 以上寻找策略与最开始的策略有了天壤之别, 而这就是简单重复性所带来的冲击, 重复性也能导致复杂性.
