从前有座山, 山上有座庙, 庙里有个老和尚在给小和尚讲故事: "从前有座山, 山上有座庙, 庙里有个老和尚在给小和尚讲故事: ..."
反复而纠结的定义
看完这个故事, 对递归你已经有了印象, 很好, 这样已足够. 如果你不幸是个喜欢精确定义的人, 那么答案可能无法让你满意:
你想知道递归是什么, 你得先知道什么是递归.
To understand recursion, you must understand recursion.
把你绕晕了没有? 你可能想这叫啥子定义哟. 如果你去谷歌英文页搜索"recursion", 谷歌就会给你来这么一下:
谷歌说: "你是说递归吗? (Did you mean: recursion)".
拼写绝对是正确的, 这不过是谷歌给你开的"递归式"的玩笑.
说完了谷歌, 再说说必应(Bing), Bing 是什么意思呢:
Bing = Bing is not google(Bing 不是谷歌)
你还是不满意, 那再看看 GNU, GNU 又是啥呢:
GNU = GNU’s Not Unix(GNU 不是 Unix)
收敛的递归
好了, 这些无限递归可能让你有点烦闷了, 让我们看点会收敛的:

你是否想起了这样的诗句:
你站在桥上看风景
看风景的人在楼上看你
明月装饰了你的窗子
你装饰了别人的梦
--卞之琳<<断章>>
再来看看据说是 MIT 计算机系的徽标:

MIT: MASSACHUSETTS INSTITUTE OF TECHNOLOGY 麻省理工学院
麻省: 即马萨诸塞州
图上有个 lambda(λ), 至于那个 (Y F)=(F (Y F)), 有没有哪头技术大奶牛知道它是啥呢?
不太清楚这玩意是啥~但公式可参见: http://en.wikipedia.org/wiki/Fixed-point_combinator#Y_combinator
另可参考 mindhacks.cn 上的这篇康托尔, 哥德尔, 图灵--永恒的金色对角线(rev#2)(没怎么看懂~有兴趣有精力的同学可钻研看看. )
自相似性(self-similarity)
下面是一颗自然界的完全二叉树(A complete binary tree in nature, 来自http://www.cs.haifa.ac.il/~shlomit/, 作者摄于非洲)

下图为芒德布罗集(**Mandelbrot set), 是分形(Fractal)**理论中的一个概念:

这个图很好体现了一种自相似性, 实际上, 不断放大这个图会发现模式在不断重复.
来自优酷的这个视频展示了这一点: http://v.youku.com/v_show/id_XMTc3NzIyMjI0.html
内容来自数学科教影片<<维度: 数学漫步>> http://www.dimensions-math.org/Dim_ZH_si.htm
如果你有兴趣, 还有另一部<<混沌: 数学漫步>>http://www.chaos-math.org/zh-hans
其它示例
艾舍尔版画(来自http://www.guokr.com/blog/50805/)
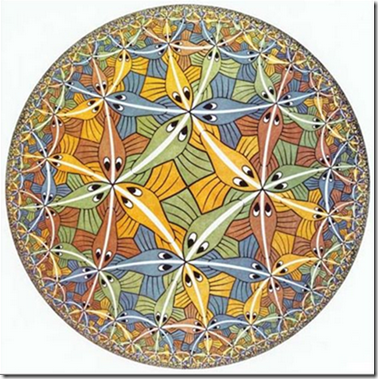
这里的艾舍尔就是那本<<哥德尔, 艾舍尔, 巴赫--集异璧之大成>>(Gödel, Escher, Bach: an Eternal Golden Braid)中的艾舍尔了.
见http://book.douban.com/subject/1291204/
我发现此书英文版居然早在 1979 年就出版了, 作者 Douglas Hofstadter 还取了个中文名叫"侯世达".
下图则为电影<<盗梦空间>>(Inception)中的一幕(其实这种场景在理发店也很常见~):

电影情节中的梦中梦也颇有递归的意味.
制造递归
如果你有个可移动的摄像头, 让屏幕上播放摄像头实时拍摄的画面, 然后拿着摄像头对准屏幕, 就能得到类似下图中的效果:
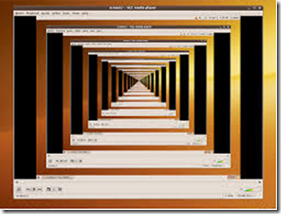
你可以想想, 为什么会这样呢?
与此相似的一个例子是音箱的爆音, 在一些会场, 有时会不小心把麦克风对谁了音箱, 大功率音箱一开始存在一些很小的电流声, 这些声音被麦克风捕获又传入音箱再次放大又传到麦克风上...很快就会演变成刺耳的尖锐声.
程序中的递归
文件夹的递归结构:
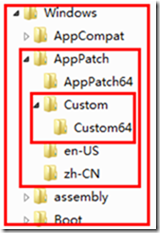
所以, 用递归去处理这些是很常见的情形. 类似的还包括那些有着树形结构特点的如 XML, HTML
以及 Chrome 浏览器中 window 对象的自指递归:
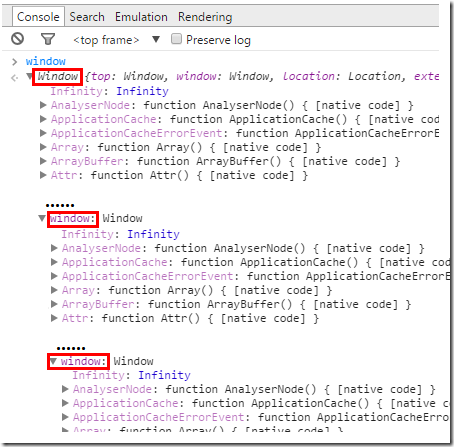
window对象是 javascript 在浏览器端的扩展中的全局对象(类似 node.js 中的global), 它里面又包含了一个名为window的属性指向它自身, 所以可以像上图那样无限展开.遍历处理这种结构需要特别小心, 否则很可能会收到 stack overflow 的错误~
以上谈了不少的例子, 都没有涉及具体的编程, 是想让大家对递归有一个直观的印象先, 后面会谈到一些经典的例子, 如阶乘以及菲波那契数列, 还有用递归来做排序(如简单的冒泡排序), 最后将展示一个用递归方式来计算换零钱种数的例子(比如用 100 元, 换成 50, 20, 10, 5, 1 元的组合总共有几种), 从中可以体现递归的优势.
由于篇幅有限, 这些将在后续篇章中谈及.
